PERSAMAAN KUADRAT (3) : JENIS AKAR, JUMLAH DAN HASIL KALI AKAR, MENYUSUN PERSAMAAN BARU
Menentukan Jenis Akar-Akar Persamaan Kuadrat dengan Diskriminan
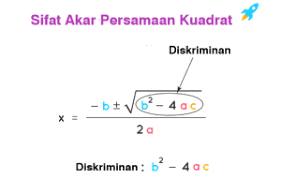
Perhatikan rumus abc berikut:
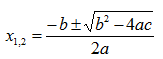
Pada rumus tersebut terdapat bentuk (b2 – 4ac) disebut diskriminan (D). Sifat akar-akar persamaan kuadrat dapat ditinjau dari nilai diskriminan, yaitu D = b2 – 4ac. Sifat akar-akar tersebut adalah.
a. Jika D > 0
- Jika D > 0 maka persamaan kuadrat ax2 + bx + c = 0 mempunyai 2 akar riil yang berlainan.
- Jika D berbentuk kuadrat sempurna dan D ≠ 0 maka persamaan kuadrat memiliki 2 akar riil berlainan dan rasional jika a, b, dan c bilangan rasional.
- Jika D bukan bentuk kuadrat sempurna dan D ≠ 0 maka memiliki 2 akar riil berlainan dan irasional
c. Jika D = 0 maka persamaan kuadrat ax2 + bx + c = 0 memiliki 2 akar riil yang sama.
Contoh:
1. Tentukan jenis akar-akar persamaan kuadrat berikut, tanpa terlebih dahulu menentukan akar-akarnya.
a. 2x2 + 3x – 14 = 0
c. 4x2 – 12x + 9 = 0
Jawab:
a. 2x2 + 3x – 14 = 0
Dengan nilai a = 2, b = 3, c = –14 maka
D = 32 – 4 ・ 2 ・ (–14)
= 9 + 112
= 121
Oleh karena D > 0 maka persamaan kuadrat 2x2 + 3x – 14 = 0 mempunyai 2 akar riil yang berbeda.
b. 2x2 + 3x + 4 = 0
Dengan nilai a = 2, b = 3, c = 4 maka
D = 32 – 4 ・ 2 ・ 4
= 9 – 32
Oleh karena D < 0 maka persamaan kuadrat 2x2 + 3x + 4 = 0 tidak mempunyai akar riil.
c. 4x2 – 12x + 9 = 0
Dengan nilai a = 4, b = –12, c = 9 maka
D = (–12)2 – 4 ・ 4 ・ 9
= 144 – 144
= 0
Oleh karena D = 0 maka persamaan kuadrat 4x2 – 12x + 9 = 0 mempunyai 2 akar kembar.
Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat

a. Jumlah akar-akar persamaan kuadrat
x1 + x2 =
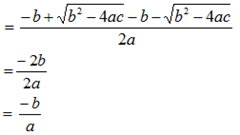
Jadi, rumus jumlah akar-akar persamaan kuadrat adalah:

b. Hasil kali akar-akar persamaan kuadrat
x1 . x2 =

Bentuk-bentuk simetri akar-akar persamaan kuadrat
1) x12 + x22 = (x1 + x2)2 – 2x1x2 (jumlah kuadrat akar-akar)
2) x13 + x23 = (x1 + x2)3 – 3x1x2 (x1+x2)
Contoh:
Diketahui x1, x2 merupakan akar-akar dari persamaan kuadrat x2 – 3x + 5 = 0, tentukan nilai dari:
a. x1 + x2
b. x1 ・ x2
c. x12 + x22
d.
Jawab
x2 – 3x + 5 = 0
Dengan nilai a = 1, b = –3, c = 5, maka
b. x1 ・ x2 = 5/1 = 5
c. x12 + x22 = (x1 + x2)2 – 2x1x2
=( 3)2 – 2.5
= 9 – 10
= -1
d.

Menyusun Persamaan Kuadrat Baru
Untuk rumus pertama yakni jika diketahui nilai dari akar-akarnya, maka persamaan kuadrat baru dapat diperoleh dengan cara memasukkan atau mensubstitusi nilai dari akar-akarnya yang telah diketahui ke dalam persamaan berikut:

Apabila diketahui jumlah dan hasil kali dari akar-akar persamaan kuadrat tersebut tanpa mengetahui nilai dari masing-masing akar-akarnya, maka kita dapat membentuk persamaan kuadrat baru menggunakan rumus berikut (rumus kedua):

Contoh:
1. Tentukan persamaan kuadrat yang akar-akarnya -1 dan 5!
Penyelesaianya:
misalkan x1 = -1 dan x2 = 5 maka persamaan kuadratnya
x2 – (x1 + x2)x + x1x2 = 0
x2 – (-1 + 5)x + (-1)(5) = 0
x2 – 4x - 5 = 0
2. Diketahui akar-akar persamaan kuadrat adalah dan . Persamaan kuadrat baru yang akar-akarnya dan adalah
Pembahasan:
Berdasarkan persamaan kuadrat baru , maka dan . Maka jumlah dan hasil kali akar-akarnya adalah

Misalkan akar-akar dari persamaan kuadrat baru adalah dan , yakni

Selanjutnya, carilah jumlah dan hasil kali dari akar-akar persamaan kuadrat baru yakni

Dengan demikian, kita peroleh
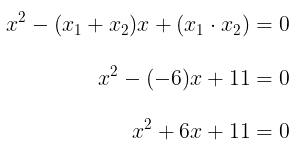




Komentar
Posting Komentar