BAB 3 TRANSFORMASI GEOMETRI (REFLEKSI DAN TRANSLASI)

-

  

mobil berubah bentuk menjadi robot


Masih ingatkah kalain pada tokoh Optimus, Bumblebee dan Megatron pada film TRANSFORMERS?

Di film itu menceritakan perubahan kendaraan (mobil atau tank) menjadi sebuah robot yang memiliki senjata untuk mengalahkan musuh. Kalau kendaraan menjadi robot artinya melakukan perubahan apa?

Yap, tepat sekali. Perubahan bentuk. Jadi, fokusnya Transformer ialah kemampuan melakukan perubahan bentuk dari kendaraan menjadi robot.

Nah Sekarang kita akan membahasnya secara matematis. 

Perubahan apa yang terjadi dalam transformasi ?

Secara umum Transformasi didefinisikan sebagai  perubahan posisi dan perubahan ukuran suatu bentuk geometri karena suatu operasi tertentu

Transformasi teterbagi atas 4 jenis, secara singkat dugambarkan dalam tabel berikut


Hari ini kita bahas 2 dulu, yaitu REFLEKSI (Pencerminan) dan TRANSLASI (Pergeseran)

Yuk kita mulai

1. Refleksi (Pencerminan)

Refleksi atau pencerminan merupakan satu jenis transformasi yang memindahkan setiap titik pada suatu bidang dengan mengggunakan sifat bayangan cermin dari titik-titik yang dipindahkan.

Seperti halnya saat kalian bercermin pada cermin datar, maka bentuk nya tidak berubah, namun posisinya menjadi terbalik

Tangan kanan di cermin menjadi tangan kiri, kaki kanan jadi kaki kiri dan seterusnya


Jika diketahui sebarang titik dengan koordinat (x, y) pada koordinat kartesius, maka koordinat bayangan hasil pencerminannya dapat dilihat

 1. Pencerminan terhadap SUMBU X



Segitiga ABC dicerminkan terhadap sumbu X, hasil bayangannya adalah segitiga A3B3C3

Pencerminan terhadap sumbu X artinya ibarat Sumbu X sebagai cermin

Jadi :

- Titik A berjarak 9 satuan di atas sumbu X, maka bayangannya adalah A3 berada 9 satuan di bawah sumbu X  
- Titik B berjarak 3 satuan di atas sumbu X, maka bayangannya adalah B3 berada 3 satuan di bawah sumbu X
- Titik C berjarak 3 satuan di atas sumbu X, maka bayangannya adalah C3  berada 3 satuan di bawah sumbu X

Titik Kordinat

Refleksi (Pencerminan) Terhadap Sumbu X

A(3, 9)

A3(3, -9)

B(3, 3)

B3(3, -3)

C(6, 3)

C3(6, -3)


2. Pencerminan terhadap SUMBU Y












Segitiga ABC dicerminkan terhadap sumbu Y, hasilnya bayangannya adalah segitiga A2B2C2

Pencerminan terhadap sumbu Y artinya ibarat Sumbu Y sebagai cermin

Jadi :

- Titik A berjarak 3 satuan di kanan sumbu Y, maka bayangannya adalah A2 berada 3 satuan di kiri sumbu Y 
- Titik B berjarak 3 satuan di kanan sumbu Y, maka bayangannya adalah B2 berada 3 satuan di kiri sumbu Y
- Titik C berjarak 6 satuan di atas sumbu Y, maka bayangannya adalah C2  berada 6 satuan di kiri sumbu Y

Titik Kordinat

Refleksi (Pencerminan) Terhadap Sumbu Y

A(3, 9)

A2(-3, 9)

B(3, 3)

B2(-3, 3)

C(6, 3)

C2(-6, 3)


3. Pencerminan Terhadap Garis y  = x

Diketahui segi empat ABCD yang memiliki koordinat di A (-1, -1), B (1, 0), C (-1, 2) dan D (-2, 1) direfleksikan terhadap garis y = x. Gambar ABCD dan bayangannya yang direfleksikan terhadap garis y = x. Bandingkan koordinat titik-titik ABCD dengan koordinat bayangannya. 
Pencerminan Terhadap Garis y = x

Penyelesaian: 

Untuk menentukan bayangan titik-titik segi empat ABCD, perhatikan jarak titik B ke garis y = x. Dari titik B buat garis yang tegak lurus ke garis y = x (disebut garis BB’) kemudian dapatkan titik B’ yang memiliki jarak yang sama besar dengan jarak titik B ke garis y = x. Titik B’merupakan bayangan titik B hasil refleksi terhadap garis y = x. Dengan demikian diperoleh koordinat B’ (0, 1). Gunakan cara yang sama, sehingga diperoleh koordinat bayangan untuk titik-titik yang lainnya sebagai berikut: 

A (–1, –1) → A’ (–1, –1) 

B (1, 0) → B’ (0, 1) 

C (–1, 2) → C’ (2, –1)  

D (–2, 1) → D’ (1, –2) 

Hubungkan keempat titik sehingga membentuk segi empat A’B’C’D’. 

4. Pencerminan Terhadap Garis y  = -x

Hasil pencerminan terhadap garis y = -x akan menghasilkan bayangan (-y, -x), agar lebih cepat paham perhatikan gambar berikut ini.

Pencerminan Terhadap Garis y = -x
Jadi jika sebuah titik koordinat P (1,2) direfleksikan terhadapa garis y = -x akan dihasilkan bayangan P' (-2, -1).

5. Pencerminan Terhadap Garis y  = k

Untuk pencerminan terhadap garis y = h kita bisa memahami dengan baik jika kita mampu membuat garis cermin y = k. Di mana nilai h merupakan bilangan asli bisa 1, 2, 3, ... atau -1, -2, -3 dan seterusnya. Untuk lebih jelasnya perhatikan gambar berikut.

Pencerminan Terhadap Garis y = k

Misalnya titik A (2, 1) direfleksikan terhadap garis y = 2, maka akan  dihasilkan bayangan pada titik A' (2, 3). Nilai 3 diperoleh dari 2k - b, di mana nilai k = 2  dan b = 1 sehingga 2 x 2 - 1 = 3.

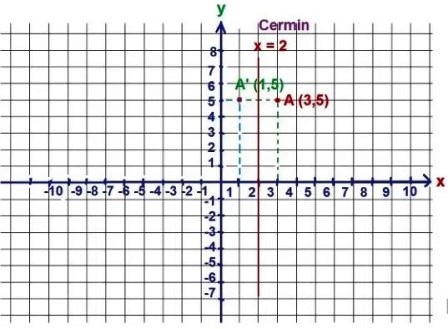
6. Pencerminan Terhadap Garis x  = h

Penceminan terhadap garis x = h sebenarnya tidak jauh berbeda dengan pencerminan terhadap sumbu -x. Hanya saja pada pencerminan garis x = h, nilai tidak sama dengan nol. Untuk lebih jelasnya perhatikan gambar berikut.
Pencerminan Terhadap Garis x = h
Pada gambar di atas cermin berada pada x = 2, berarti nilai h = 2. Koordinta titik A (3,5) direfleksikan terhadap garis x = 2 diperoleh bayangan A' (1,5). Dari mana diperoleh A' (1,5)? diperoleh dari rumus pencerminan garis x =  h,yaitu ( 2h - x, y) berarti ( 2 x 2 - 3, 5) = ( 1,5).


2. Translasi (Pergeseran)


Translasi merupakan jenis transformasi yang memindahkan suatu titik sepanjang garis lurus dengan arah dan jarak. Artinya, translasi itu hanya perpindahan titik 

Gambaran translasi itu seperti ini 

contoh gambar translasi

 (sumber: rumushitung.com)

Translasi itu hanya berubah posisinya saja. Bentuk dan ukurannya tetap sama. 

Sekarang perhatikan gambar berikut 

Segitiga JKL di translasikan (digeser) sejauh 3 satuan ke kanan dan 4 satuan ke bawah 

menjadi segitiga J'K'L'


Sehingga perubahan titik koordinatnya adalah 

Titik Kordinat

Translasi (Pergeseran) 3 satuan ke kanan dan 4 satuab ke bawah

J(-1, 3)

J'(2, -1)

K(-1, 1)

K'(2, -3)

L(-4, 1)

L'(-1, -3)


Rumus umum translasi

 

Demikian penjelasan dari Ibu

Untuk Rotasi dan Dilatasi insyaaAllah kita sambung minggu depan

Bisa dipahami ya

Gampang kok, tinggal gambar di buku strimin kalian

Nanti koordinat bayangannya otomatis ketemu


Oke untuk menguji pemahaman kalian, cobalah latihan berikut di buku striminmu

Latihan ini sekaligus sebagai rangkuman kalian dan selanjutnya Ibu jadikan sebagai bahan 

evaluasi

Kerjakan di buku strimin kalian

Selamat berlatih

SEMANGAT...


1. Gambarlah bangun PQRS dengan P(-7,7) , Q(-5,9) , R(-3,7) dan S(-5,3)

2. Bangun apakah yang terbentuk ?

3. Refleksikan (cerminkan) bangun tersebut terhadap sumbu Y

4 Gambar kembali bangun PQRS pada bidang koordinat yang berbeda, kemudian translasikan (geser) bangun tersebut 7 satuan ke kanan dan 3 satuan ke bawah

5  Berdasarkan hasil gambarmu, isilah tabel berikut :

Titik Kordinat

Refleksi (Pencerminan) Terhadap Sumbu Y

Translasi (pergeseran) 7 satuan ke kanan dan 3 satuan ke bawah

P(-7,7)

 

 

Q(-5,9)

 

 

R(-3,7)

 

 

S(-5,3)

 

 

 










Komentar

Posting Komentar

Postingan populer dari blog ini

ARITMETIKA 3 : BUNGA TUNGGAL, BRUTO, NETO, DAN TARA

-
Gambar
  BUNGA TUNGGAL, BRUTO, NETO, DAN TARA 1. Menentukan Bunga Tunggal Di lingkungan sekitar kita, sering kita jumpai bahwa seseorang membeli mobil  secara angsuran dengan  bunga  10% pertahun atau seseorang meminjam uang  di bank dengan  bunga  2% per bulan. Secara umum  bunga  dapat diartikan sebagai jasa berupa uang yang diberikan  oleh pihak peminjam kepada pihak yang meminjamkan modal atas persetujuan  bersama. Ada kalanya juga  bunga  dapat diartikan sebagai jasa berupa uang yang  diberikan oleh pihak bank kepada pihak yang menabung atas persetujuan  bersama Dalam menentukan besarnya bunga bank, ditentukan oleh : a.         Lamanya menabung/peminjaman b.        Besar bunga tabungan/pinjaman dalam waktu tertentu c.         Besarnya tabungan awal/modal ( uang semula ) Sehingga besarnya bunga tunggal bisa menggunaka...
Baca selengkapnya

BAB 1 BILANGAN BERPANGKAT

-
Gambar
  Bilangan Berpangkat: Pengertian dan Sifatnya Pengertian Bilangan Berpangkat Bilangan berpangkat atau Perpangkatan adalah perkalian berulang dari suatu bilangan yang sama. Bilangannya dapat berupa bilangan pangkat bulat positif, nol atau bulat negatif. Bentuk umum dari perpangkatan adalah a n      = a × a × a × … × a,  dengan n bilangan bulat positif dan a sebanyak jumlah n Contoh, perpangkatan 3 seperti di bawah ini: 3 × 3 × 3 × 3 × 3 = 3 5 3 5  adalah perpangkatan 3. 3 disebut sebagai bilangan pokok (basis) sedangkan 5 sebagai pangkat (eksponen). Perhatikan contoh-contoh berikut: a.    2x2x2x2 = 2 4  hasilnya 16 b. 3x3x3x3x3 = 3 5  hasilnya 243 c. (-5)x(-5) = (-5) 2  hasilnya 25 d. (-7)x(-7)x(-7) = (-7) 3  hasilnya -343 (negatif 343) e.  3 + 2 ×   5 2       3 + 2 ×   5 2   = 3 + 2 ×   25           Lakukan operasi perkalian ...
Baca selengkapnya

BAB 1 : BENTUK AKAR (Pertemuan ke-2)

-
Gambar
  BENTUK AKAR Bentuk  akar merupakan akar dari suatu bilangan yang hasilnya bukan bilangan rasional atau merupakan bilangan irasional.  Bentuk akar merupakan bentuk lain untuk menyatakan bilangan berpangkat. Bentuk akar termasuk dalam bilangan irasional, yakni bilangan yang tidak dapat dinyatakan dengan pecahan a/b, a dan b bilangan bulat a dan b ≠ 0. Bilangan bentuk akar merupakan bilangan yang terdapat di dalam tanda "√" disebut tanda akar. Beberapa contoh bilangan irasional dalam bentuk akar adalah √2, √6, √7, √11 dan lain-lain. Sedangkan √25 bukan bentuk akar hal ini karena √25 = 5  (5 adalah bilangan rasional). Seperti halnya bilangan berpangkat, bilangan bentuk akar juga memiliki sifat-sifat tertentu. Sifat-sifat ini akan memudahkan dalam melakukan operasi aljabar yang melibatkan bentuk akar.  Sifat-sifat bentuk akar  meliputi: Lalu bagaimana caranya menyederhanakan akar suatu bilangan bulat? Kita dapat menggunakan faktor-faktor dari bilangan yang aka...
Baca selengkapnya